基本的な二次ベジェ曲線
二次ベジェ曲線(Quadratic Bezier Curve)は始点・終点・制御点(1つ)を指定して描く曲線です。
react-native-skiaのPathで二次ベジェ曲線を描くにはquadTo(またはrQuadTo)を使います。
quadTo(制御点x, 制御点y, 終点x, 終点y)
const path = Skia.Path.Make()
path.moveTo(20, 150)
path.quadTo(180, 20, 280, 170)
<Canvas>
<Path path={path} style="stroke" color="lightblue" strokeWidth={3} />
</Canvas>
SVGのようにコマンド文字列(Qコマンド)を指定して記述することもできますが、上記のようにSkPathオブジェクトを生成してメソッドを呼び出していく方が可読性が良く制御もしやすくなります。
この上のベジェ曲線の構造を視覚化すると以下のようになります。
上の点が制御点です。開始点から制御点までの中間点と、制御点から終了点までの中間点を線でつなげると、その中心が曲線の湾曲の頂点になります。
二次ベジェ曲線を滑らかにつなげる
二次ベジェ曲線を描いた後、元の制御点と対象的な位置を制御点に指定して更に二次ベジェ曲線を描くと滑らかに繋がる曲線を表現することができます。
const start1 = { x: 10, y: 150 }
const control1 = { x: 80, y: 50 }
const end1 = { x: 150, y: 150 }
const path = Skia.Path.Make()
path.moveTo(start1.x, start1.y)
path.quadTo(control1.x, control1.y, end1.x, end1.y)
const control2 = {
x: control1.x + (end1.x - control1.x) * 2,
y: control1.y + (end1.y - control1.y) * 2,
}
path.quadTo(control2.x, control2.y, 290, 40)
このベジェ曲線の構造を可視化すると以下になります。
2つ目の曲線の制御点が、曲線の接続地点から見て1つ目の曲線の制御点と対象的な位置に配置されているのがわかります。
SVGのTコマンドで同様のことができるのですが、React Native Skiaでは同様のコマンドを行うためのメソッドは見当たりませんでした。ですので対象となる制御点の位置を自分で計算して曲線をつなげる必要があります。
また、この滑らかな曲線を応用し連続でつなげていけば波も描くことができます。
const start = { x: 10, y: 150 }
const distance = 40
const waveHeight = 20
const path = Skia.Path.Make()
path.moveTo(start.x, start.y)
for (const i of [0, 1, 2, 3, 4, 5, 6]) {
path.rQuadTo(distance / 2, waveHeight * (i % 2 === 0 ? -1 : 1), distance, 0)
}
曲線をアニメーションさせる
最後に曲線をアニメーションさせてみたいと思います。まず動かない状態で途中まで曲線を引いてみます。
以下は曲線を60%まで引いた例です。
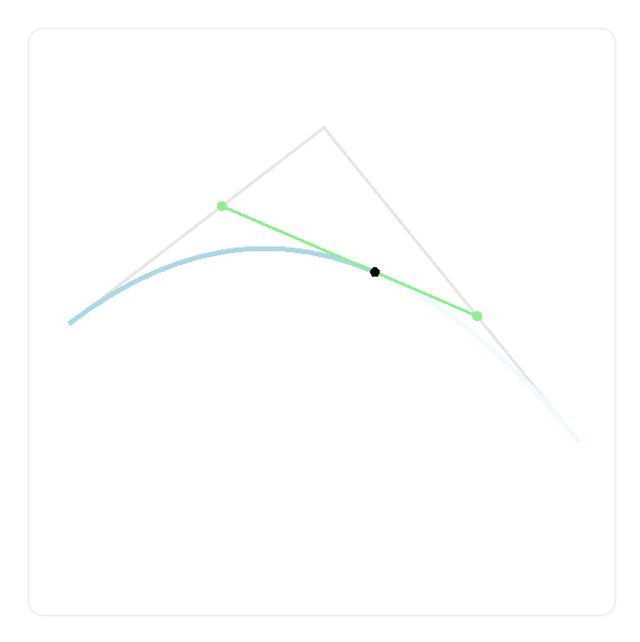
途中までの曲線を引くにはまず開始点と制御点、制御点と終点の間で進捗に応じて進んだ点(黄緑の点)を取得します。更に2つの点の間で同様に進捗に応じた点(黒の点)を取得します。この点が曲線の終点になります。
この最初の中間点(黄緑)を制御点とし、最後に取得した点(黒)を終点に指定して二次ベジェ曲線を引くと、元の曲線の途中までの曲線を引くことができます。
進捗を動的に変化させることでアニメーションできます。
function getVector(p1: { x: number; y: number }, p2: { x: number; y: number }) {
return {
x: p2.x - p1.x,
y: p2.y - p1.y,
}
}
const start = { x: 20, y: 150 }
const control = { x: 150, y: 50 }
const end = { x: 280, y: 210 }
const subPath = Skia.Path.Make()
subPath.moveTo(start.x, start.y)
subPath.quadTo(control.x, control.y, end.x, end.y)
export default function AnimatedQuadCurve() {
const progress = useTiming({ loop: true }, { duration: 4000 })
const curvePath = useComputedValue(() => {
const vector1 = getVector(start, control)
const vector2 = getVector(control, end)
const point1 = {
x: start.x + vector1.x * progress.current,
y: start.y + vector1.y * progress.current,
}
const point2 = {
x: control.x + vector2.x * progress.current,
y: control.y + vector2.y * progress.current,
}
const vector3 = getVector(point1, point2)
const point3 = {
x: point1.x + vector3.x * progress.current,
y: point1.y + vector3.y * progress.current,
}
const path = Skia.Path.Make()
path.moveTo(start.x, start.y)
path.quadTo(point1.x, point1.y, point3.x, point3.y)
return path
}, [progress])
<Canvas>
<Path
path={subPath}
style="stroke"
color="rgb(230, 230, 230)"
strokeWidth={1.5}
/>
<Path
path={curvePath}
style="stroke"
color="lightblue"
strokeWidth={2.5}
/>
</Canvas>
}
この記事のサンプルのソースコードはこちらで確認できます。